Linear Graphs
Linear graphs are so-named because they are straight lines.
Coordinates are read from the origin (0,0). They are in order of x-coordinate (horizontal) and y-coordinate (vertical).
Because they are straight lines, only 3 points are needed. Two points are needed to draw the line, and the third point is used to check for correctness.
Graphs do not always pass through the origin (0,0).
Linear Equations are written in the form of:
y = mx + c
where
m is the gradient (slope)
c is the y-intercept (point where the graph cuts the y-axis)
m and c are both constants (fixed numbers).
Examples are:
- In the equation y = 3x + 2, the gradient is 3 and the y-intercept is 2.
- In the equation y = 4x – 5, the gradient is 4 and the y-intercept is –5.
- In the equation y = 1⁄2 x + 6, the gradient is 1⁄2 or 0.5 and the y-intercept is 6.
- In the equation y = x, the gradient is 1 and the y-intercept is 0.
More information about gradient and the y-intercept is at Analytical Geometry.
Example One - Buying Motorbike Race Tickets

Motorbike race tickets cost $50 each. Draw a table of values and a linear graph showing the cost of the tickets.
Answer:
Because this graph is a straight line, only 3 points are needed - two points for drawing the line, and the third for checking correctness.
Choose x = 0, 1, 2 unless the question states otherwise.
| Number of tickets | 0 | 1 | 2 |
| Cost of tickets | $ 0 | $ 50 | $ 100 |

Example Two - Graph of y = x
(a) In the linear equation y = x, what is the gradient?
(b) What is the y-intercept?
(c) Draw a table of values and the graph of the linear equation y = x
Answer:
(a) Gradient = 1
(b) y-intercept = 0
(c) Because this graph is a straight line, only 3 points are needed - two points for drawing the line, and the third for checking correctness.
Choose x = 0, 1, 2 unless the question states otherwise.
| x | 0 | 1 | 2 |
| y = x | 0 | 1 | 2 |
| Working | y = x y = 0 | y = x y = 1 | y = x y = 2 |
| Coordinates | (0,0) | (1,1) | (2,2) |
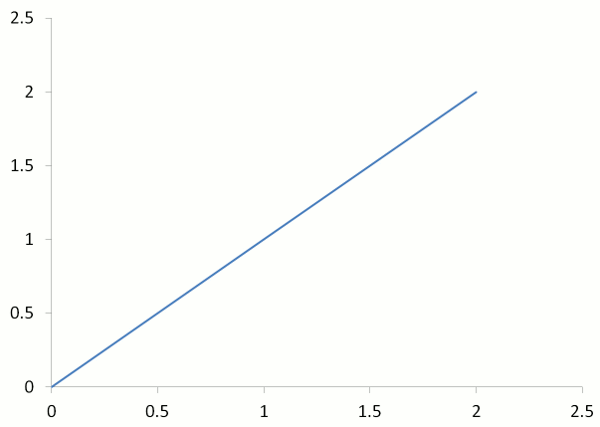
Example Three - Graph of y = 2x
(a) In the linear equation y = 2x, what is the gradient?
(b) What is the y-intercept?
(c) Draw a table of values and the graph of the linear equation y = 2x
Answer:
(a) Gradient = 2
(b) y-intercept = 0
(c) Because this graph is a straight line, only 3 points are needed - two points for drawing the line, and the third for checking correctness.
Choose x = 0, 1, 2 unless the question states otherwise.
| x | 0 | 1 | 2 |
| y = 2x | 0 | 2 | 4 |
| Working | y = 2x y = 2 × 0 y = 0 | y = 2x y = 2 × 1 y = 2 | y = 2x y = 2 × 2 y = 4 |
| Coordinates | (0,0) | (1,2) | (2,4) |

Example Four - Graph of y = 2x + 3
(a) In the linear equation y = 2x + 3, what is the gradient?
(b) What is the y-intercept?
(c) Draw a table of values and the graph of the linear equation y = 2x + 3
Answer:
(a) Gradient = 2
(b) y-intercept = 3
(c)
| x | 0 | 1 | 2 |
| y = 2x + 3 | 3 | 5 | 7 |
| Working | y = 2x + 3 y = 2 × 0 + 3 y = 3 | y = 2x + 3 y = 2 × 1 + 3 y = 5 | y = 2x + 3 y = 2 × 2 + 3 y = 7 |
| Coordinates | (0,3) | (1,5) | (2,7) |

Questions
What do you notice about the slope of the graphs of y = 2x and y = 2x + 3?
Example Five - Graph of y = 1⁄2 x + 1
(a) In the linear equation y = 1⁄2 x + 1, what is the gradient?
(b) What is the y-intercept?
(c) Draw a table of values and the graph of the linear equation y = 1⁄2 x + 1
Answer:
(a) Gradient = 1⁄2
(Notice that the graph is steeper than y = 1x but not as steep as y = 2x and y = 2x + 3)
(b) y-intercept = 1
(c)
| x | 0 | 1 | 2 |
| y = 1⁄2 x + 1 | 1 | 11⁄2 | 2 |
| Working | y = 1⁄2x + 1 y = 1⁄2 × 0 + 1 y = 1 |
y = 1⁄2x + 1 y = 1⁄2 × 1 + 1 y = 11⁄2 |
y = 1⁄2x + 1 y = 1⁄2 × 2 + 1 y = 2 |
| Coordinates | (0,1) | (1,11⁄2) | (2,2) |
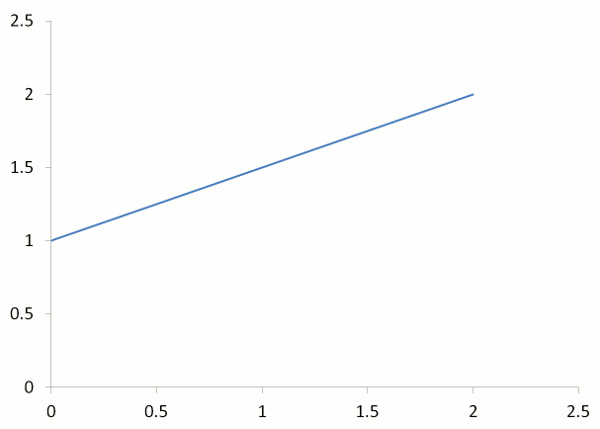
Questions
What do you notice about the coefficient of x (the number multiplied by x) and the steepness of the graph?
What do you notice about the constant (the number at the end of the equation) and the point where the graph intersects with the y-axis?
Example Six - Graph of y = 3x – 1
(a) In the linear equation y = 3x – 1, what is the gradient?
(b) What is the y-intercept?
(c) Graph the equation y = 3x – 1 where –2 < x < 2
Answer:
(a) Gradient = 3 (Notice that the graph is steeper than y = 1x, y = 2x and y = 2x + 3)
(b) y-intercept = –1
(c) The question specified that 3 values of x must be between –2 and 2. Choose x-values of –2, 0, 2.
| x | –2 | 1 | 2 |
| y = 3x – 1 | –7 | 1 | 3 |
| Working | y = 3x – 1 y = 3 × (–2) – 1 y = –6 – 1 y = –7 |
y = 3x – 1 y = 3 × 0 – 1 y = 0 – 1 y = –1 |
y = 3x – 1 y = 3 × 2 – 1 y = 4 – 1 y = 3 |
| Coordinates | (–2,–7) | (0,–1) | (2,3) |

Question
Draw a table of values and then graph the equation y = 4x – 3 where –3 < x < 3
(Remember that your graph will be correct if it is a straight line.)
Example Seven - Graph of y = –2x + 5 (Negative Gradient)
(a) In the linear equation y = –2x + 5, what is the gradient?
(b) What is the y-intercept?
(c) Graph the equation y = –2x + 5
Answer:
(a) Gradient = –2 (Notice that the graph is backwards.)
(b) y-intercept = 5
(c)
| x | 0 | 1 | 2 |
| y = –2x + 5 | 5 | 3 | 1 |
| Working | y = –2x + 5 y = (–2) × 0 + 5 y = 0 + 5 y = 5 |
y = –2x + 5 y = (–2) × 1 + 5 y = (–2) + 5 y = 3 |
y = –2x + 5 y = (–2) × 2 + 5 y = (–4) + 5 y = 1 |
| Coordinates | (0,5) | (1,3) | (2,1) |


| 
| 
|